Testing Super Mario Using a Behavior Model Autonomously (Part 1)

Written ByVitaliy Zakaznikov
Share It

Autonomous testing is one of the most powerful approaches for exploring vast state spaces in complex systems. Rather than manually writing test cases for every scenario, autonomous systems can systematically explore millions of states, discovering edge cases that human testers would never think to check.

In this two-part follow-up, we’ll continue the Super Mario Bros. testing series by implementing the autonomous testing approach presented by Antithesis, where they autonomously play and beat the game. Later in Part 2, we’ll plug in the behavior model we developed in Part 1 and Part 2 of our first series to validate correctness in real-time during autonomous exploration. In the process, we demonstrate the true power of autonomous testing and behavior models: systematically exploring massive state spaces while writing your validation once, then plugging it into any testing driver—including our very own autonomous system that discovers new paths while validating behavior at every step.

Here’s what we’re aiming for—implement our own autonomous state space exploration that will allow Mario to complete levels of Super Mario Bros. without any human guidance:


Autonomous exploration: Completing Level 1

The complete implementation is open source and available in our Examples/SuperMario repository. Clone the code and let’s dive into how autonomous state space exploration works!

1
git clone --branch v2.0 --single-branch https://github.com/testflows/Examples.git && cd Examples/SuperMario

The proposed approach

Antithesis’s article presents a surprisingly simple yet powerful algorithm for autonomous exploration of Super Mario. At its core is a mutation-based input generator that randomly flips input bits to create variations:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import mario
import random

def generate_input(starting_byte, flip_probability, input_length):
    input = []
    next_byte = starting_byte
    
    for _ in range(input_length):
        for j in range(8):
            if random.random() < flip_probability:
                next_byte ^= (1 << j)
        input.append(next_byte)
    
    return input

This random mutation approach treats game inputs (right, left, jump, action, down, enter) as bytes, where each bit represents whether a given key is pressed (1) or not (0). The algorithm randomly flips individual bits with a small probability (typically around 10%) by XORing the current input with a random mask—flipping bits where the mask is 1 while preserving bits where the mask is 0. By flipping bits, the algorithm generates variations of input sequences, exploring different paths through the game.


Input: Random input generation

The reason behind choosing this input generation algorithm is that it better mimics how the game is meant to be played: the currently pressed key is likely to remain pressed in the next frame while another key can be added at the same time. For example, you hold down the right key while also pressing the jump or action buttons.

However, the random input generation is not enough. The reason is that Mario moving randomly will inevitably cause it to die by running into enemies or falling into pits. Therefore, the exploration itself can never be one-shot. Instead, you have to store traveled paths (input sequences) and have a strategy to pick a sequence for the next iteration. These travel paths effectively define Mario’s state because the game is deterministic.

The system is said to be deterministic only if given the same input you will always get the same output.

Therefore, starting from the same position and applying the same input sequence will always lead to the same Mario position in the game. This means when we pick a traveled path, we can replay it and then try to continue it with new mutations.

The path selection requires a fitness function. For Super Mario, a simple criterion is to favor paths with the highest x-axis position, since winning the game requires advancing to the right. However, always picking the path with the highest fitness score doesn’t work—there will be many cases where the path ends in a state from which no further exploration is possible. For example, right before touching a Goomba, or being in the air right before falling into a pit. Such states are not recoverable and lead to dead ends.

To overcome this problem, it’s not enough to keep just the best path we’ve found so far. Instead, we need to maintain a collection of paths with different fitness scores and use a probability distribution function to pick the next path to explore. This way, we’re more likely to pick paths with higher scores while still giving paths with lower scores a chance to be explored.


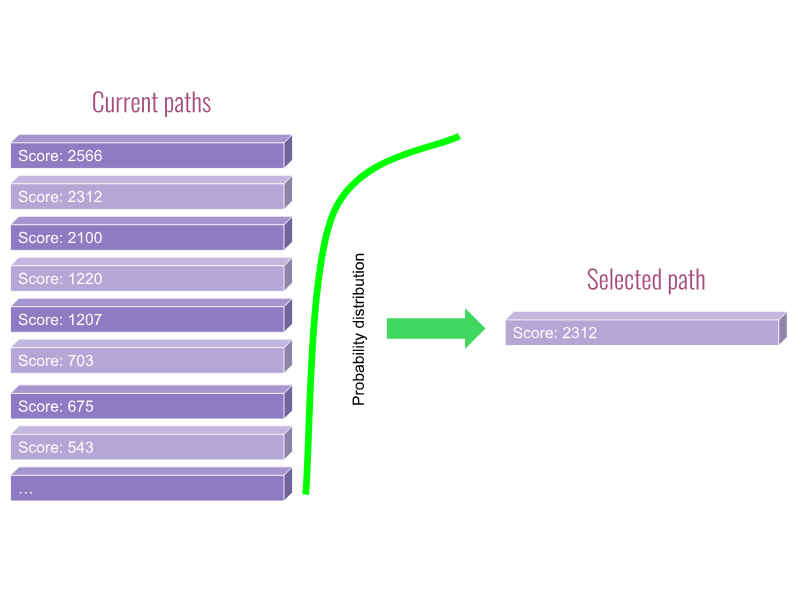
Paths: Selecting path

The beauty of this state space exploration approach lies in its simplicity. You don’t need to understand the game’s mechanics or hand-craft complex strategies. The mutation process naturally discovers interesting behaviors through random exploration, guided by fitness scoring that rewards progress through the game world.

Characteristics of the proposed approach

Let’s step back and examine how the proposed exploration system works:

  • We generate random input by flipping bits with small probability (typically ~10%), producing a sequence of button presses
  • We build a path by recording the input sequence along with a score quantifying how far Mario progresses (for Super Mario, based on x-axis position)
  • We store these paths in a collection, maintaining a population of different trajectories through the game
  • We select a path using a probability distribution function that favors higher-scoring paths while still giving lower-scoring paths a chance
  • Determinism enables resuming in exactly the same state: because the game always produces identical results for the same input sequence, we can replay any stored path to reach that specific game state, then continue exploring from there with new mutations
  • This cycle of select→replay→mutate→evaluate repeats continuously, systematically exploring the state space by building on previously discovered paths

Comparing the approach to Genetic Algorithm

Let’s see how these characteristics map to a canonical Genetic Algorithm:

Our System GA Concept
Collection of stored paths Population of individuals
Input sequence (button presses) Genotype encoding behavior
Game state (Mario position, score) Phenotype (observable result)
Progress scoring function Fitness function
Path probability distribution selection function Selection with elite bias
Bit-flip input generation Mutation operator
— Crossover (recombination)
Each exploration iteration Generation cycle

Applying the broad understanding of these concepts, without nit-picking, the proposed approach is essentially a Genetic Algorithm—maintaining a population, scoring fitness, selecting promising candidates, and mutating them to explore variations.

However, a skeptic might raise two concerns: the absence of crossover, and whether an input sequence truly qualifies as a genotype.

Genotype mapping

Let’s address the genotype question first. In traditional GAs, genotypes often encode multiple behavioral strategies that apply broadly: “jump more often,” “play aggressively,” “avoid edges.” In our system, the input sequence encodes something more specific: the ability to reach a particular state. But this is a form of behavioral encoding! Our input sequences are genes that enable reaching specific game states—a valid specialization of the general multi-gene GA framework where each path represents a complete behavioral strategy for reaching a specific position.

Absence of crossover

As for the absence of crossover, it’s important to understand what crossover actually is: an evolutionary optimization technique that progresses the population by recombining currently present genetic material. Crossover combines beneficial traits from different individuals to potentially create better offspring without requiring new mutations. However, crossover is not strictly required—it’s an evolutionary optimization, not a fundamental requirement. Mutation alone can effectively explore the state space, particularly when paths build incrementally as in our case. Therefore, the proposed approach remains a valid GA, just one that currently relies solely on mutation for variation rather than using both mutation and crossover for evolution.

Why this maps to Genetic Algorithms?

The fact that this state space exploration technique maps perfectly to a Genetic Algorithm is not a coincidence—it reveals something fundamental about both testing and evolution.

When exploring complex state spaces, you need:

  • A way to maintain progress (population of paths)
  • A way to focus on promising areas (selection by fitness)
  • A way to discover new possibilities (mutation)
  • A way to reach specific states (genes as enablers)

This is exactly what biological evolution does. Genes aren’t just instructions—they’re traits that enable organisms to reach and survive in environmental states not yet mastered by the population. Our input sequences serve the same role: enabling Mario to reach game states not yet explored.

One might question whether GA truly applies to deterministic systems where the same inputs always produce the same results. However, determinism actually makes GAs more powerful by providing perfect reproducibility. We can define non-determinism as simply not having control over all inputs—apparent randomness is often just hidden state. Deterministic systems like Super Mario make this explicit, giving us perfect reproducibility for controlled evolutionary experiments.

Recognizing the approach as a mutation-based Genetic Algorithm unlocks decades of evolutionary computation research and opens a wide range of possibilities.

Concrete implementation of autonomous exploration

Unfortunately, the original article did not present a concrete implementation. Since the approach is essentially a Genetic Algorithm, there are countless variations to explore in how we generate inputs, select paths, score progress, and manage stored paths. After some trial and error, we’ve settled on the following implementation—by no means optimal, but sufficient to demonstrate that the approach works.

The core state exploration loop is implemented in autonomous play test, which orchestrates the entire process. The test repeatedly selects promising paths from stored paths, replays them to specific game states, then extends them with new generated inputs—continuously discovering and expanding reachable regions of the state space.

Here is the top level loop of the algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
path = self.context.paths.select()  # Start with the most promising path

# Break exploration into intervals (evolution epochs) to refresh path selection
for part in range(play_seconds // interval):       
    for i in range(tries):  # Try extending the same path multiple times
        with Scenario(f"interval {part}-{i}"):
            stop_index = path.select_stop_index()  # Pick resume point (usually near end)
            # Replay path to that point, then extend with new generated inputs
            play(
                path=path,
                play_seconds=interval,
                with_model=with_model,
                stop_index=stop_index,
            )
        if path not in self.context.paths.paths:  # Path led to death?
            break  # Stop trying this path, move to next one
    self.context.paths.clean()  # Remove redundant paths with similar progress
    path = self.context.paths.select()  # Select next path (favoring higher scores)

This elegant loop captures the essence of systematic state space exploration, organized into exploration intervals (epochs) that structure the discovery process. Within each epoch: select a path based on its score, replay it to a chosen state, extend it with generated inputs, then evaluate the results. Paths that lead to death are immediately pruned from the population, focusing effort on viable states. At each epoch boundary, the population of the stored paths is cleaned to remove redundant paths, and a new path is selected—this periodic reassessment prevents the algorithm from getting stuck while ensuring each promising path gets multiple attempts. This structure embodies the core Genetic Algorithm cycle: maintaining a population (stored paths), scoring fitness, selecting promising candidates, introducing variation through mutation (varying the resume point and generated inputs, without crossover), and letting natural selection (death pruning) drive evolution toward increasingly successful paths.

Let’s examine each component in detail.

Input generation

Input generation is implemented using weighted move selection. We use a hybrid approach that balances pure exploration with structured gameplay patterns. The key insight here is that random mutations alone can be too chaotic—Mario needs some coherent action sequences to make meaningful progress. By combining weighted fuzzy mutations with predefined move patterns, we get the best of both worlds: the ability to discover unexpected solutions through randomness, and the efficiency of human-like movement patterns that naturally fit the game’s mechanics.

  • Fuzzy mutation: 5% bit-flip probability with 10× selection weight (fuzzy generator) enables pure exploration that can discover unconventional solutions, like precise timing sequences that bypass enemies.
  • Predefined moves: patterns like walk_right_long, jump_up_right_high_action spanning 5-120 frames (move library) provide coherent action sequences that mimic natural gameplay and accelerate early progress.
  • Directional bias: right moves weighted 2×, left moves 0.5× naturally aligns exploration with the game’s primary objective of progressing rightward through the level.

Path selection

Path selection is implemented in the selection function. The selection strategy must balance exploitation (using our best discoveries) with exploration (trying less promising paths that might break through plateaus). A naive “always pick best” strategy fails when the best path leads to an unrecoverable state. Our exponential weighting gives the best path strong preference while maintaining a diverse population of alternatives.

  • Best path preference: 50% base probability plus exponential weighting ensures we heavily exploit our most successful discoveries without getting trapped.
  • Exponential decay for alternatives: Remaining probability distributed among other paths using exponential weighting maintains diversity and prevents convergence to local maxima—occasionally exploring “worse” paths can reveal breakthrough strategies.

Scoring

Scoring is calculated by the scoring function. The scoring function defines what “success” means and guides the entire evolutionary state space exploration process. We use a hierarchical structure with powers of 10 to create clear priorities: completing a level is worth infinitely more than any position within a level, reaching further right is worth more than doing it faster. The formula level_num × 10⁹ + x_pos × 10³ + (999 - time) ensures these priorities never conflict—a path that completes level 2 will always score higher than any path still in level 1, regardless of how fast or far the latter progresses.

Backtracking and splitting

Backtracking and splitting are handled by backtracking and splitting functions. When Mario dies, we don’t want to discard the entire path—there’s often valuable progress hidden within failed attempts. Backtracking removes the dangerous final frames, giving us a safer starting point. Splitting goes further by extracting the highest-scoring intermediate state, preserving Mario’s best position even if later moves led to disaster. This salvaging mechanism significantly accelerates exploration by retaining hard-won progress.

  • Backtracking: Remove last frames before death, creating a safer checkpoint by rewinding before the fatal mistake.
  • Splitting: Extract the intermediate high-scoring point, preserving peak progress even when the path ends poorly—for example, saving Mario’s farthest position before he fell into a pit.

Death state pruning

Death state pruning is enforced by stored paths management and in the play loop. Dead ends are evolutionary dead weight. By aggressively pruning any path that ends in death and immediately deleting replayed paths that fail, we maintain a population of only viable starting points. This creates intense selection pressure that prevents the population from being diluted with paths that can’t possibly contribute to finding the solution. It’s harsh, but effective—survival of the fittest in action.

Path resuming and mutation

Path resuming is implemented in the play function. Rather than always replaying a path to its end, we use a triangular distribution to occasionally resume from earlier points along the path. This implements mutation by varying where we branch off from existing paths—we might try different continuations from the same intermediate state, potentially discovering better alternatives. The high mode value means we usually resume near the end (small mutations), but the occasional early resumption (large mutations) prevents us from getting stuck always trying to extend from the same final state.

Path cleaning

Path cleaning is performed by the cleaning function. As the stored paths population grows, many paths become redundant—slightly different input sequences that reach nearly the same position. Keeping all of them wastes computational resources and dilutes selection pressure. By grouping paths within position ranges and keeping only the best from each group, we maintain a diverse population while eliminating near-duplicates. This compression prevents the population from exploding with marginally different strategies that offer no real diversity.

Autonomous exploration in action

With the above autonomous test in place we can start exploring Super Mario state space.

Here is the basic command to run our autonomous play test:

1
python3 tests/run.py --autonomous --play-seconds 300

With default settings (20-second intervals, 3 tries per interval), this creates 15 epochs with 3 exploration attempts each. Since we must replay paths from the beginning to reach selected states, the actual runtime varies based on path lengths—expect 15-30 minutes for a 5-minute exploration session.

Here’s an example run that completed in 22 minutes:

1
2
3
4
5
  ⟥    [note] All end scores: [1002836976, 1002453959, 1002334961, 1002058957, 1001942961, 1001763981, 1001595956, 1001398975, 1001234983, 1000966985, 1000835964, 1000729959, 1000393959, 1000108963, 1000004963, 0]
  ⟥    [note] Best end score: 1002836976
  ⟥    [note] Selected path score: 1002836976 (index 0)
  
✔ [ OK ] '/super mario/autonomous/play' (22m 21s)

The population contains 16 paths with varying scores, demonstrating the diversity maintained by our cleaning strategy. Our best score of 1002836976 decodes as:

  • Level: 1 (first 3 left digits)
  • X-position: 2836 pixels (middle 5 digits)
  • Time: 23 seconds (999 - 976)

This means Mario successfully progressed 2836 pixels into Level 1—approximately 70% of the level’s total distance—demonstrating that autonomous exploration can make substantial progress without domain knowledge.

Performance optimization through instrumentation

Replaying paths to reach specific states for each exploration attempt introduces significant overhead. Since our reference implementation doesn’t include save/resume functionality (checkpointing), we must replay from the beginning each time—a practical constraint that slows exploration.

To accelerate the process, we’ve instrumented the game with two key capabilities:

  • Level selection (--start-level): Start exploration directly at any level with full lives, allowing us to focus on specific level challenges without replaying earlier sections.
  • Accelerated speed (--fps 300): Run the game 5× faster than the default 60 fps—dramatically speeding up path evaluation. The algorithm works at normal speed too, but without checkpointing support, the replay overhead makes higher frame rates practical for faster iteration.

These test instrumentation techniques are standard practice in real-world testing scenarios and essential for making autonomous exploration practical. In production testing environments, we routinely instrument systems to control initial states, accelerate time, inject faults, and manipulate conditions—it’s how effective testing gets done.

Finding a path to complete Level 1

After some trial and error—as expected with probabilistic search techniques—we found that these parameters significantly speed up finding a solution:

1
python3 tests/run.py --autonomous --play-seconds 3000 --fps 300 --always-pick-best-path --start-level 1 --paths-file level1_paths.json --backtrack 0
  • --fps 300: Runs 5× faster while staying within game loop latency limits
  • --always-pick-best-path: Focuses on the highest-scoring path; stop-index mutation provides enough variation to avoid getting stuck
  • --start-level 1: Begins exploration directly at Level 1, skipping the intro screens
  • --paths-file level1_paths.json: Stores discovered paths for this level independently
  • --backtrack 0: Turns off backtracking since stop-index mutation already explores alternative branches

This shifts toward exploitation (best path) over exploration (diverse population), which works well when targeting a specific level.

Here is a video of us beating Level 1:

Level 1 proved relatively straightforward—the algorithm consistently discovered the underground pipe shortcut that bypasses most of the level’s obstacles. Excellent work, Mario!

Finding a path to complete Level 2

Level 2 uses the same parameters with a fresh paths file to explore independently:

1
python3 tests/run.py --autonomous --play-seconds 3000 --fps 300 --always-pick-best-path --start-level 2 --paths-file level2_paths.json --backtrack 0

Level 2 proved more challenging due to increased presence of pits, diverse enemies (Goombas, Koopas, Piranha Plants), and moving platforms. The high fps setting provided an unexpected advantage—Mario’s invincibility period appeared extended, allowing rapid progress through dangerous sections. Despite the difficulty, our exploitation-focused strategy (always picking the best path with stop-index mutation, no backtracking) successfully discovered a winning path.

Finding a path to complete Level 3

Continuing with Level 3, which was the harder level to complete.

1
python3 tests/run.py --autonomous --play-seconds 3000 --fps 300 --always-pick-best-path --start-level 3 --paths-file level3_paths.json --backtrack 0

Level 3 features numerous paths that lead to Mario’s death—he must precisely jump from platform to platform across large gaps while avoiding enemies. The combination of precise jumping and enemy avoidance made finding a winning path significantly harder. Nevertheless, Level 3 was beaten, and the video above shows our autonomous Mario’s successful run. Autonomous testing for the win again!

Finding a path to complete Level 4

Our reference Python implementation of Super Mario contains 4 levels, making Level 4 the final challenge for our autonomous exploration test:

1
python3 tests/run.py --autonomous --play-seconds 3000 --fps 300 --always-pick-best-path --start-level 4 --paths-file level4_paths.json --backtrack 0

Level 4 revealed an interesting bug (which could be caused by our high FPS hack)—colliding with a Fire Bar renders Mario invisible, allowing him to bypass all remaining obstacles and reach the level’s end. Bug or not, the algorithm found its way to the end, demonstrating how autonomous state space exploration can uncover unexpected behaviors that would be hard to find using classical testing techniques.

Conclusion

We’ve successfully demonstrated the effectiveness of Antithesis‘s autonomous exploration approach using our reference Python implementation of Super Mario Bros. After analyzing the approach, we connected it to Genetic Algorithms, revealing the evolutionary computation structure underlying the exploration. Our implementation completed all four levels without human guidance, discovering shortcuts, navigating complex enemy patterns, mastering precise jumping, and even uncovering a potential collision bug in Level 4.

However, there’s a critical limitation: our fitness function only measures progress (x-position, level completion), not correctness. We don’t validate whether Mario’s velocity follows expected physics, whether jumps have valid causes, whether falling happens only without ground support, or whether movements are causally justified by game state. While Antithesis played the original NES game and we used a Python implementation, this distinction becomes crucial for correctness validation—checking proper behavior requires access to internal game variables (velocity, collision state, key presses) beyond just Mario’s x,y position.

In the behavior model series (Part 1 and Part 2), we developed a comprehensive behavior model with causal, safety, and liveness properties that validate game correctness frame-by-frame. In Part 2 of this autonomous testing series, we’ll integrate that model directly into the exploration loop, validating every frame in real-time. This combination is powerful: autonomous exploration discovers vast state spaces, while the behavior model ensures correctness throughout—finding not just winning paths, but correctness bugs hiding in edge cases.

Stay tuned for Part 2, where autonomous exploration meets rigorous correctness validation!